https://www.acmicpc.net/problem/9251
9251번: LCS
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net

이 문제는 DP에서 계속 다뤘었던 부분 증가 수열의 최대 길이를 구하는 문제와 비슷하지만
그냥 증가 부분 수열이 아닌, 두 문자열의 부분 수열의 최대 길이를 구하는 문제이다.
롸 너무 어렵다
또 구글링함...ㅋ
참고한 포스팅은 이거다.
https://happylsm76.tistory.com/entry/%EB%B0%B1%EC%A4%80-9251%EB%B2%88LCS-with-Python
[백준] 9251번(LCS) with Python
문제 www.acmicpc.net/problem/9251 9251번: LCS LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP
happylsm76.tistory.com
LCS(Longest Common Subsequence) 알고리즘
1. 개요 LCS란 Longest Common Subsequence의 약자로 최장 공통 부분 문자열이다. 우리가 알고 있는 substring과 비교하면 substring은 연속된 부분 문자열이고 subsequence는 연속적이지는 않은 부분 문자열이다.
twinw.tistory.com
이해가 안가서 여러 포스팅을 보고 푼 문제이다.
일단 풀이 코드는 다음과 같다.
풀이코드)
s1 = list(input())
s2 = list(input())
dp = [[0]*(len(s1)+1) for i in range(len(s2)+1)]
for i in range(1, len(s2)+1):
for j in range(1, len(s1)+1):
if s2[i-1] == s1[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i][j-1], dp[i-1][j])
print(dp[-1][-1]) # 최대값
전체적인 흐름을 살펴보자면,
두 문자열 중에서 하나의 문자열은 그대로 두고
나머지 한 문자열의 처음부터 마지막 문자까지 반복문을 통해 비교하는 것이다.
두 문자열 s1, s2가 있다고 하자.
나는 s1을 기준으로 하고 s2의 문자 하나하나를 s1과 비교해가며 탐색했다.
(두 문자열이 바뀌어도 상관x)

s2 CAPCAK에서
C부터 차례대로 s1인 ACAYKP와 비교했다.
비교했을 때 문자가 같으면 1을 올려주었다.
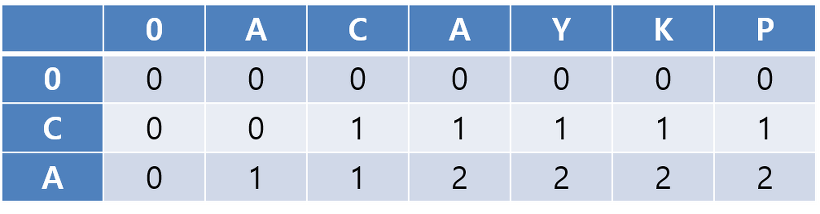
이건 ACAYKP와 CA를 비교한 결과이다.
반복문은 A만 떼와서 비교하지만, 앞서 C에 대한 탐색이 끝난 상태이므로, 그 탐색 결과에 A의 탐색 결과를 이어붙임으로
써 결론적으로는 CA를 비교했을 때 올 수 있는 부분 수열의 최대 길이를 저장한 표이다.
이를 위해서 DP 배열 선언시 각 행과 열을 각각 문자열의 길이만큼 생성해주면 된다.
풀이 코드에서는 문자열의 길이 +1 만큼 해줬는데, 반복문에서 1부터 돌리기 위해서 그렇게 했다.
이런 식으로 계속 이어 붙여나가며 탐색하면 된다.
키 포인트는
앞에서 탐색한 결과를 DP에 저장함으로써, 그 값을 다음 반복문을 돌 때 이용하는 것이다.
두 문자열에서 문자를 비교할 때, 값이 같으면 전 값에 +1을 해주고
문자가 다를 경우엔, 그 전의 값(같은 행 이전 열), (같은 열 이전 행) 둘 중에서 최대를 가져온다.
같은 행 이전 열은 혹시나 이전에 같은 문자가 나와 값이 올라갈 경우가 있고,
같은 열 이전 행은 이전 탐색(이전 부분 수열)의 결과이기 때문에 이어 받아야 한다.
결론적으로는 최대 길이를 구하는 것이므로 둘 중 최대 값만 가져오면 된다.
구현은 단순한데.. 다시 풀라고 하면 못 풀 것 같당..쩝,,,
'코딩 문제' 카테고리의 다른 글
| 백준 1629 - 곱셈 (0) | 2023.01.26 |
|---|---|
| 백준 12865 - 평범한 배낭 (0) | 2023.01.23 |
| 백준 2565 - 전깃줄 (0) | 2023.01.18 |
| 백준 11504 - 가장 긴 바이토닉 부분 수열 (0) | 2023.01.17 |
| 백준 11053 - 세상에서 제일 긴 증가하는 부분 수열 (0) | 2023.01.16 |