https://www.acmicpc.net/problem/1149
1149번: RGB거리
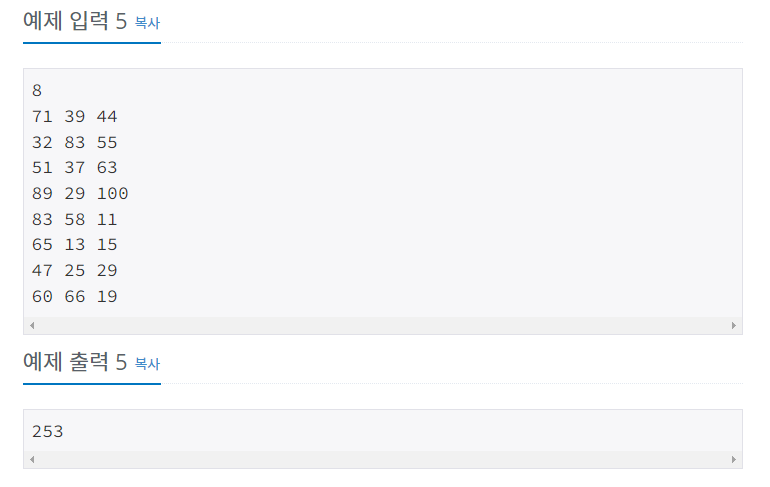
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
이 문제는 서로 이웃된 집들의 색이 겹치지 않게 칠할 때, 그 최소비용을 구하는 문제이다.
코드를 짜긴 했는데 예제 1~4까지는 정답이 나왔지만, 예제 5에서 오답이 나왔다.
틀린 코드를 리뷰해보자면
def find_case(flag):
if flag == 0:
return [1, 2]
elif flag == 1:
return [0, 2]
elif flag == 2:
return [0,1]
n = int(input())
h = []
dp = []
flag = 0
tmp = 0
case = []
for i in range(n):
h.append(list(map(int, input().split())))
for i in range(3):
s = 0
flag = i
s += h[0][flag]
for j in range(1,n):
case = find_case(flag)
tmp = min(h[j][case[0]], h[j][case[1]])
s += tmp
if tmp == h[j][case[0]]:
flag = case[0]
else:
flag = case[1]
dp.append(s)
print(min(dp))나는 일단 3가지 경우의 수로 나누어 생각하려고 했다.
첫 번째 집이 1. 빨강 2. 초록 3. 파랑
그리고 어쨋든 최소 비용을 구하는거니까 I번째 집이 색깔을 고르면 I+1번째 집은 I번째 집이 고른 색깔을 제외하고 나면 2가지 경우의 수가 남는데, 그 경우의 수 중 최소 비용을 더하면 되는 줄 알았다.
그래서 알고리즘 흐름을 정리해보자면, I번째 집이 칠한 색깔을 flag에 넣고 find_case 함수를 만들어 i+1번째 집이 칠할 수 있는 경우의 수를 반환하고 또 최소 비용의 색깔로 칠한 후 그 색깔을 flag에 넣고 함수를 또 호출하여 계속 다음 집으로 넘기며 비용을 구하는 흐름이다.
하지만, 내가 간과하던 것이 있었다.
바로, 예제 5번처럼 최소비용이 각 라인의 최소값으로만 이루어지지 않을 경우이다.
이웃된 집과 똑같은 색을 칠할 수 없다는 조건 때문에 =>
즉,이웃된 집과 똑같은 색깔의 비용이 매우 작거나/
굳이 최소 비용만 고르지 않아도 위와 같은 조건 때문에 더 작은 비용이 나올 수도 있다.
결국엔 모든 경우의 수를 따져보아야 한다.
그래서 알고리즘에 심각한 오류가 있음을 인지하고 바로 구글링함ㅋ
정답코드는 아래와 같다.
n = int(input())
cost = []
dp = [[0]*3 for i in range(n)]
for i in range(n):
cost.append(list(map(int, input().split())))
dp[0][0], dp[0][1], dp[0][2] = cost[0][0], cost[0][1], cost[0][2] # 첫 번째 집의 rgb 비용 초기화
for i in range(1, n):
dp[i][0] = min(dp[i-1][1] + cost[i][0], dp[i-1][2] + cost[i][0]) # i번째가 R일때 i집까지의 최소비용
dp[i][1] = min(dp[i - 1][0] + cost[i][1], dp[i - 1][2] + cost[i][1]) # i번째가 G일때 i집까지의 최소비용
dp[i][2] = min(dp[i - 1][0] + cost[i][2], dp[i - 1][1] + cost[i][2]) # i번째가 B일때 i집까지의 최소비용
print(min(dp[n-1]))이 문제도 첫 번째 집부터 최소비용을 구하며 끌고 가야되는 문제이므로 dp를 적용한다.
cost는 각 집들의 비용을 담아둔 리스트이고
dp는 각 집까지의 최소비용을 담아둘 리스트이다.
dp는 총 n개의 집의 3가지 경우의 수를 따져볼 것이므로, n*3크기의 배열로 초기화하였다.
dp[i][0] : i번째 집이 빨강일 경우의 i번째 집까지의 최소비용
dp[i][1] : i번째 집이 초록일 경우의 i번째 집까지의 최소비용
dp[i][2] : i번째 집이 파랑일 경우의 i번째 집까지의 최소비용
따라서,
dp[0][0] : 첫 번째 집이 빨강일 경우의 최소비용
dp[0][1] : 첫 번째 집이 초록일 경우의 최소비용
dp[0][2] : 첫 번째 집이 파랑일 경우의 최소비용
이렇게 되고, 이는 첫 번째 집이므로 그냥 첫 번쨰 집의 각 색에 따른 비용과 같다.
dp[0][0] = cost[0][0] # 비용 초기화
dp[0][1] = cost[0][1]
dp[0][2] = cost[0][2]따라서 이렇게 초기화가 필요하다.
나는 다시 풀 때도 초기화를 빼먹어서 오답이 나왔었다.
두 번째로 봐야할 것은 반복문이다.
for i in range(1, n):
dp[i][0] = min(dp[i-1][1] + cost[i][0], dp[i-1][2] + cost[i][0]) # i번째가 R일때 i집까지의 최소비용
dp[i][1] = min(dp[i - 1][0] + cost[i][1], dp[i - 1][2] + cost[i][1]) # i번째가 G일때 i집까지의 최소비용
dp[i][2] = min(dp[i - 1][0] + cost[i][2], dp[i - 1][1] + cost[i][2]) # i번째가 B일때 i집까지의 최소비용1부터 n-1까지 반복문을 돌면서 각 집의 3가지 경우의 수에 따른 최소 비용을 구한다.
dp[i][0] = min(dp[i-1][1] + cost[i][0], dp[i-1][2] + cost[i][0]) # i번째가 R일때 i집까지의 최소비용맨 처음에는 이 코드를 보고 ?했었는데 말로 쉽게 설명해보자면,
i번째 집이 빨강일 경우 i번째 집까지의 최소비용은
=>
i-1번째 집이 초록일 경우 i-1번째 집까지의 최소비용 + i번째가 빨강일 경우의 비용
i-1번째 집이 파랑일 경우 i-1번째 집까지의 최소비용 + i번째가 빨강일 경우의 비용
이 두가지 비용 중 최소값을 픽하면 된다.
그러면 결국, 모든 경우의 수에 대하여 고려가 가능하다.
예를 들어보자.
dp[1][0] = min(dp[0][1] + cost[1][0], dp[0][2] + cost[1][0])
dp[1][1] = min(dp[0][0] + cost[1][1], dp[0][2] + cost[1][1])
dp[1][2] = min(dp[0][0] + cost[1][2], dp[0][1] + cost[1][2])위 코드는 2번째 집 (인덱스는 1)이 각 RGB일 때의 2번째 집까지의 최소비용을 구하는 코드이다.
두 번째 집이 빨강일 경우만 살펴보자면.
첫 번째 집이 초록일 경우의 비용 + 두 번째 집이 빨강일 경우의 비용
첫 번째 집이 파랑일 경우의 비용 + 두 번째 집이 빨강일 경우의 비용
이 두가지 경우의 수 중 더 작은 것이 두번째 집이 R일 경우의 두 번째 집까지의 최소비용이 되는 것이다.
이러한 반복문을 통해, 첫 번째 집부터 n번째 집까지의 최소비용을 구할 수 있다.
그럼 n번째 집이 R, G, B일 경우의 n번째까지 칠할 경우의 최소비용을 구할 수 있고
그 3가지 경우에서 가장 작은 값이 최소비용이 되는 것이다.
따라서 반복문을 다 돌린 다음 dp의 n-1번째 리스트만 보면 된다.
그것이 최종 최소비용들이기 때문이다.
'코딩 문제' 카테고리의 다른 글
| 백준 2579 - 계단 오르기 (0) | 2023.01.13 |
|---|---|
| 백준 1932 - 정수 삼각형 (0) | 2023.01.12 |
| 백준 1912 - 연속합 (0) | 2023.01.11 |
| 백준 1904 - 01 타일 (0) | 2023.01.11 |
| 백준 14889 - 스타트와 링크 (0) | 2023.01.10 |