https://www.acmicpc.net/problem/24479
24479번: 알고리즘 수업 - 깊이 우선 탐색 1
첫째 줄에 정점의 수 N (5 ≤ N ≤ 100,000), 간선의 수 M (1 ≤ M ≤ 200,000), 시작 정점 R (1 ≤ R ≤ N)이 주어진다. 다음 M개 줄에 간선 정보 u v가 주어지며 정점 u와 정점 v의 가중치 1인 양
www.acmicpc.net
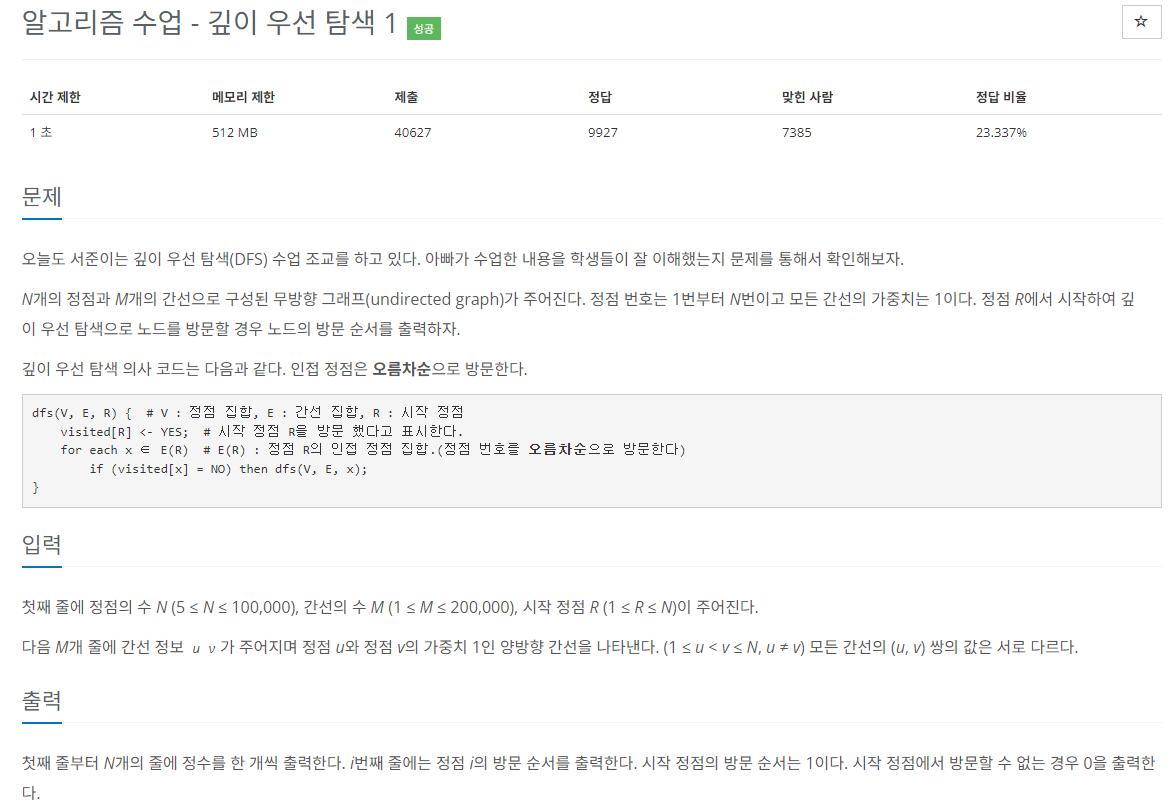

이 문제는 트리 자료구조의 DFS 알고리즘의 대표적인 기초 문제라고 볼 수 있다.
이 문제를 해결하기 위해서는 다음과 같은 정보가 필요하다.
1. 각 노드들과 인접한 노드들의 정보 → 그래야 인접한 노드들을 타고 타고 들어갈 수 있다.
2. 각 노드들의 방문 여부 → 방문하지 않은 노드만 탐색하기 위함이다.
문제에서는 1부터 N까지의 노드가 주어지기 때문에, 2차원의 리스트를 생성하여 i번 노드의 인접 노드들은 i번째 리스트에 담아 저장하도록 했다.
첫 노드부터 시작하여 해당 노드가 이미 방문된 노드인지 아닌지를 확인하고 방문하지 않은 노드라면, 해당 노드의 인접노드들을 순차적으로 다시 dfs 함수를 호출하여 방문하면 된다. (이 때도 방문 여부 확인 필수이며, 인접 노드는 오름차순으로 방문한다고 했으므로 인접 노드 탐색 전에 인접 노드 리스트에 대한 정렬 처리를 해준 후, 탐색을 시작하여야 한다.)
풀이 코드)
import sys
def dfs(start):
global cnt # 방문 순서
visited[start] = 1 # 방문 여부 변경
result[start] = cnt # 방문 순서를 저장할 리스트
graph[start].sort() # 인접 노드를 오름차순으로 방문해야 하므로
for node in graph[start]: # 해당 노드와 인접한 노드 탐색
if visited[node] == 0: # 방문하지 않은 노드라면
cnt += 1
dfs(node)
sys.setrecursionlimit(10**6) # 파이썬의 기본 재귀 깊이 제한이 1000이므로 10**6으로 늘려줌
N, M, R = list(map(int, sys.stdin.readline().strip().split()))
graph = [[] for i in range(N+1)] # i번 노드와 인접한 노드들은 배열의 i번 배열에 저장
visited = [0]*(N+1) # 방문 여부
result = [0]*(N+1) # 각 노드의 방문 순서
for i in range(M):
u, v = list(map(int,sys.stdin.readline().strip().split()))
# 각 노드와 인접한 노드를 리스트에 저장
graph[u].append(v)
graph[v].append(u)
cnt = 1 # 방문 횟수 초기화
dfs(R) # R번째 노드부터 시작
for i in range(1, len(result)):
print(result[i])
+) 추가
위의 풀이 코드를 보면, sys.setrecursionlimit(10**6)이 있다.
파이썬은 기본적으로 재귀 깊이 제한이 1000이기 때문에, 만약 1000이 넘어가는 재귀호출이 일어날 경우엔 런타임 에러가 발생한다. 따라서, 10**6으로 늘려주는 코드를 작성한 것이다. 코테에서는 반드시 써주도록 하자!
참고
'코딩 문제' 카테고리의 다른 글
| 백준 24444 - 알고리즘 수업 - 너비 우선 탐색1 (0) | 2024.04.10 |
|---|---|
| 백준 10799 - 쇠막대기 (0) | 2024.02.28 |
| 백준 1931 - 회의실 배정 (1) | 2024.02.25 |
| 백준 18258 - 큐 2 (0) | 2023.02.27 |
| 백준 10986 - 나머지 합 (0) | 2023.02.18 |